Gradient Descent Variants

Deep Learning Optimization Techniques

Optimization plays a crucial role in deep learning by helping neural networks learn the optimal set of parameters (weights and biases) to minimize the loss function. The primary goal is to find a minimum of the loss function efficiently.

1. Understanding Gradient Descent

1.1 The Core Idea

Gradient descent is an iterative optimization algorithm used to find the minimum of a function. It works by computing the gradient (derivative) of the function at a particular point and then updating the parameters in the opposite direction of the gradient.

1.2 Real-Life Example

Imagine you are standing at the top of a mountain and want to reach the lowest valley. However, there is dense fog, so you can only see a little ahead. To descend efficiently:

• You check the slope (gradient) under your feet.
• If the slope is steep, you take a larger step (move faster).
• If the slope is shallow, you take a smaller step (move slower).
• You keep repeating this process until you reach the lowest point (minimum).

This is exactly how gradient descent works in mathematics—taking small steps in the direction of the steepest descent until convergence.

2. Function Definition

We define a function f(x) that we want to minimize:

f(x)=x²

The gradient (or derivative) of this function with respect to x is:

d/dx f(x)=2x

This gradient tells us the direction and magnitude of the slope at any given point x.

Understanding the Function and Its Derivative

We have a function:

f(x)=x²

This means that for any given x, the function’s value is simply the square of x.
For example:

• If x=2, then f(2)=2²=4.
• If x=−3, then f(−3)=(−3)²=9.

2. Why Do We Need the Derivative?

The derivative (or gradient) of a function tells us how fast the function is changing at a given point. In gradient descent, we use this information to find the minimum value of the function.

3. Calculating the Derivative of f(x)=x²

The derivative of a function is found using differentiation. The rule for differentiating xⁿ is:

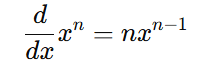
For our function:

f(x)=x²

Applying the rule:

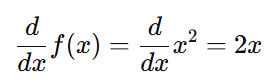
So, the gradient of f(x)=x²

This means:

• If x=2, then the gradient is 2(2)=4.
• If x=−3, then the gradient is 2(−3)=−6.

Understanding the Derivative (Gradient)

• If the gradient is positive, it means the function is increasing at that point, so we need to move left (decrease x).
• If the gradient is negative, the function is decreasing, so we move right (increase x).
• If the gradient is zero, we have reached a minimum or maximum.

For f(x)=x², the gradient is zero at x=0, meaning x=0 is the minimum.

How This is Used in Gradient Descent

1. Start at some initial value of xxx (e.g., x=10).
2. Compute the gradient: 2x.
3. Update x using the formula: x_new=x_old−α⋅2 where α\alphaα is the learning rate (controls step size).
4. Repeat until x converges to the minimum.

Example

Step 1: Define the Function and Gradient

We have:

f(x)=x²

The gradient (derivative) is:

d/dx f(x)=2x

This tells us the slope at any given x.

Step 2: Choose Initial Values

To apply Gradient Descent, we need:

• A starting value for x (we choose x=10).
• A learning rate (α), which controls how big our steps are. Let’s take α=0.1.
• A formula to update x: x_new=x_old−α⋅2x

Step 3: Iterations of Gradient Descent

Let’s manually compute a few iterations:

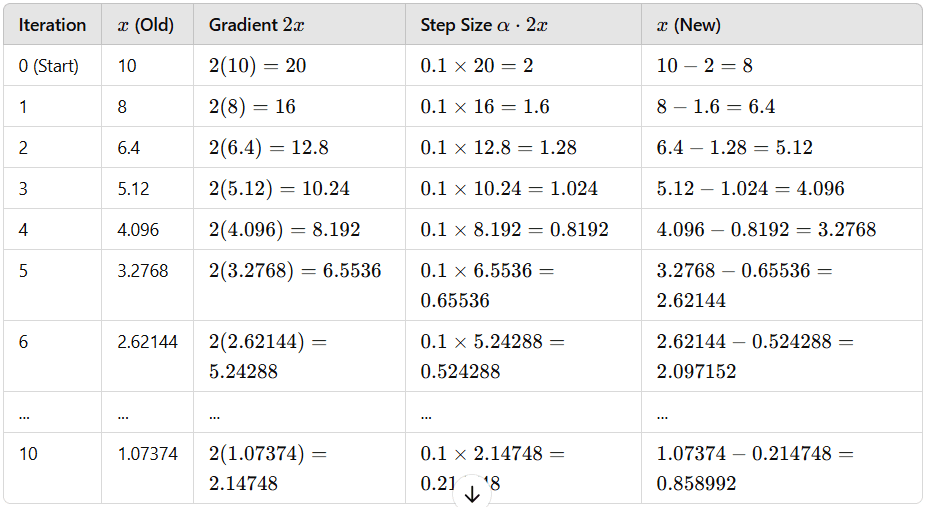
As you can see, x is decreasing and moving closer to 000, which is the minimum of f(x)=x².

Step 4: Continue Until Convergence

We keep updating xxx until the change is very small (close to zero). Eventually, x will settle near 0, which is the minimum of f(x).

Step 5: Python Code to Automate This Process

Now, let’s write Python code to do this automatically.

import numpy as np

# Function and gradient
def f(x):
    return x**2

def gradient(x):
    return 2*x

# Gradient Descent Parameters
alpha = 0.1   # Learning rate
x = 10        # Initial value
iterations = 20  # Number of iterations

# Perform Gradient Descent
for i in range(iterations):
    x = x - alpha * gradient(x)  # Update x
    print(f"Iteration {i+1}: x = {x:.6f}, f(x) = {f(x):.6f}")

print(f"\nFinal optimal x value: {x:.6f}")

Step 6: Understanding the Output

If you run the Python code, you will see output similar to:

Iteration 1: x = 8.000000, f(x) = 64.000000
Iteration 2: x = 6.400000, f(x) = 40.960000
Iteration 3: x = 5.120000, f(x) = 26.214400
Iteration 4: x = 4.096000, f(x) = 16.777216
Iteration 5: x = 3.276800, f(x) = 10.737418
Iteration 6: x = 2.621440, f(x) = 6.871948
Iteration 7: x = 2.097152, f(x) = 4.398047
Iteration 8: x = 1.677722, f(x) = 2.814750
Iteration 9: x = 1.342177, f(x) = 1.801440
Iteration 10: x = 1.073742, f(x) = 1.152922
Iteration 11: x = 0.858993, f(x) = 0.737870
Iteration 12: x = 0.687195, f(x) = 0.472237
Iteration 13: x = 0.549756, f(x) = 0.302231
Iteration 14: x = 0.439805, f(x) = 0.193428
Iteration 15: x = 0.351844, f(x) = 0.123794
Iteration 16: x = 0.281475, f(x) = 0.079228
Iteration 17: x = 0.225180, f(x) = 0.050706
Iteration 18: x = 0.180144, f(x) = 0.032452
Iteration 19: x = 0.144115, f(x) = 0.020769
Iteration 20: x = 0.115292, f(x) = 0.013292

Final optimal x value: 0.115292

Observations

• x decreases with each iteration.
• f(x)=x² also decreases, moving closer to zero.
• After 20 iterations, x is very close to 0, which is the minimum of f(x).